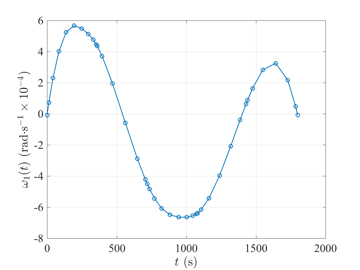
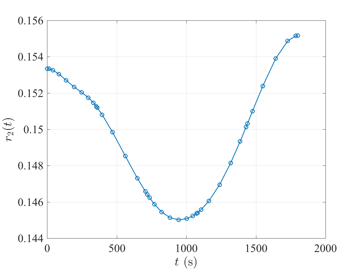
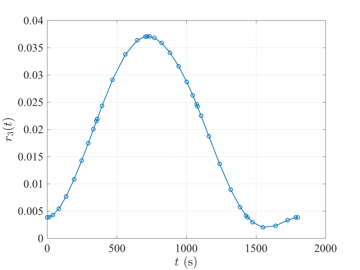
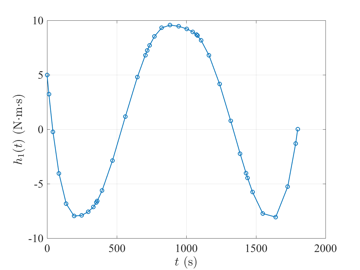
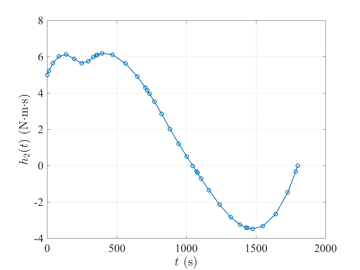
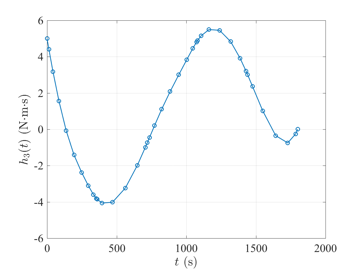
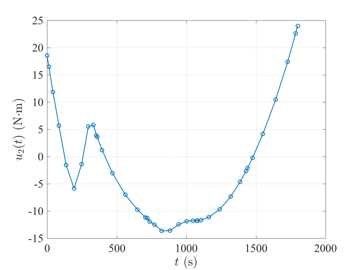
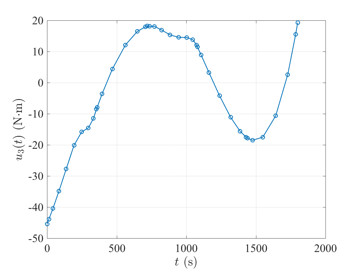
Space Station Attitude Reorientation Problem
The space station attitude reorientation optimal control problem is given as follows. Minimize the cost functional $$J={\textstyle\frac{1}{2}}\int_{0}^{t_f}\mathbf{u}^\textsf{T}(t)\mathbf{u}(t)dt$$ subject to the dynamic constraints $$\begin{array}{lcl}\dot{\boldsymbol{\omega}} & = & \mathbf{J}^{-1}\left\{\boldsymbol{\tau}_{gg}(\mathbf{r}) - \boldsymbol{\omega}^{\otimes}\left[\mathbf{J}\boldsymbol{\omega}+\mathbf{h}\right] - \mathbf{u}\right\}, \\ \dot{\mathbf{r}} & = & {\textstyle\frac{1}{2}}\left[\mathbf{r}\mathbf{r}^{\textsf{T}} + \mathbf{I} + \mathbf{r} \right]\left[\boldsymbol{\omega} - \boldsymbol{\omega}(\mathbf{r})\right], \\ \dot{\mathbf{h}} & = & \mathbf{u}, \end{array}$$ the inequality path constraint $$\|\mathbf{h}\|_2 \leq h_{\max}, $$ and the boundary conditions $$\begin{array}{lcl} t_f & = & 1800, \\ \boldsymbol{\omega}(0) & = & \bar{\boldsymbol{\omega}}_0, \\ \mathbf{r}(0) & = & \bar{\mathbf{r}}_0, \\ \mathbf{h}(0) & = & \bar{\mathbf{h}}_0, \\ \mathbf{0} & = & \mathbf{J}^{-1}\left\{\boldsymbol{\tau}_{gg}(\mathbf{r}(t_f)) - \boldsymbol{\omega}^{\otimes}(t_f)\left[\mathbf{J}\boldsymbol{\omega}(t_f)+\mathbf{h}(t_f)\right] \right\}, \\ \mathbf{0} & = & {\textstyle\frac{1}{2}}\left[\mathbf{r}(t_f)\mathbf{r}(t_f)^{\textsf{T}} + \mathbf{I} + \mathbf{r}(t_f) \right]\left[\boldsymbol{\omega}(t_f) - \boldsymbol{\omega}(t_f)(\mathbf{r}(t_f))\right]. \end{array} $$ The solution to the space station attitude control optimal control problem \(t_f=1800\) using GPOPS-II is shown in the figures below.