Dynamic Soaring Problem
The dynamic soaring optimal control problem is stated as follows. Minimize the cost functional $$J=\beta$$ subject to the dynamic constraints $$\begin{array}{lclclcl}\dot{x}(t)&=&v(t)\cos\gamma(t)\sin\psi(t) + W_x & , & m\dot{v}(t) & = & -D -mg\sin\gamma(t) -m \dot{W}_x\cos\gamma(t)\sin\psi(t), \\ \dot{y}(t) & = & v(t)\cos\gamma(t)\cos\psi(t) & , & mv(t)\dot{\gamma}(t) & = & L\cos\sigma(t) - mg\cos\gamma(t) + m\dot{W}_x\sin\gamma(t)\sin\psi(t), \\ \dot{z}(t) & = & v(t)\sin\gamma(t) &, & mv(t)\dot{\psi}(t)\cos\gamma(t) &=& L\sin\sigma(t) - m\dot{W}_x\cos\psi(t), \end{array}$$ and the boundary conditions $$\begin{array}{lcl} (x(0),y(0),z(0) & = & (0,0,0), \\ (x(t_f),y(t_f),z(t_f)) & = & (0,0,0), \\ (v(t_f),\gamma(t_f),\psi(t_f)) & = & (v(0),\gamma(0),\psi(0)+2\pi).\end{array}$$ The solution to the dynamic soaring optimal control problem using GPOPS-II is shown in the figures below.



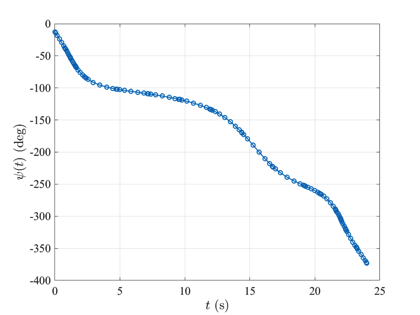
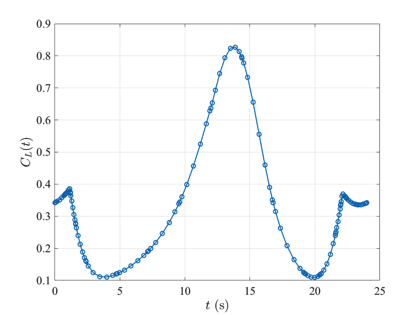

Image Courtesy of FreeDigitalPhotos.net. Photo taken by Dominic Harness. Used with Permission.

