Kinetic Batch Reactor Problem
The kinetic batch reactor optimal control problem is stated as follows. Minimize the cost functional $$ J = \gamma_1 t_f^{(3)} + \gamma_2 p$$ subject to the dynamic constraints $$ \begin{array}{lcl} \dot{y}_1^{(k)} & = & -k_2 y_2^{(k)} u_2^{(k)}, \\ \dot{y}_2^{(k)} & = & -k_1 y_2^{(k)} y_6^{(k)} + k_{-1} u_4^{(k)} -k_2 y_2^{(k)} u_4^{(k)}, \\ \dot{y}_3^{(k)} & = & k_2 y_2^{(k)} u_2^{(k)} + k_3 y_4^{(k)} y_6^{(k)} - k_{-3} u_3^{(k)}, \\ \dot{y}_4^{(k)} & = & -k_3y_4^{(k)}y_6^{(k)}+k_{-3}u_3^{(k)}, \\
\dot{y}_5^{(k)} & = & k_1 y_2^{(k)} y_6^{(k)} - k_{-1} u_4^{(k)}, \\
\dot{y}_6^{(k)} & = & -k_1 y_2^{(k)} y_6^{(k)} + k_{-1} u_4^{(k)} - k_3 y_4^{(k)} y_6^{(k)} + k_{-3} u_3^{(k)},
\end{array},\quad (k=1,2,3),$$ the equality path constraints $$ \begin{array}{lcl}
p - y_6^{(k)} + 10^{-u_1^{(k)}} - u_2^{(k)} - u_3^{(k)} - u_4^{(k)} & = & 0, \\
u_2^{(k)} - K_2 y_1^{(k)}/(K_2+10^{-u_1^{(k)}}) & = & 0, \\
u_3^{(k)} - K_3 y_3^{(k)}/(K_3+10^{-u_1^{(k)}}) & = & 0,\\
u_4^{(k)} - K_4 y_5/(K_1+10^{-u_1^{(k)}}) & = & 0,\\
\end{array}, \quad (k=1,2,3),$$ where the fifth path constraint is not enforced in phase 3, the control inequality path constraint $$ 293.15 \leq u_5^{(k)} \leq 393.15, \quad (k=1,2,3),$$ the interior-point constraints $$ \begin{array}{lcl} t_f^{(1)} & = & 0.01, \\ t_f^{(2)} & = & t_f^{(3)}/4, \\ y_i^{(k)} & = & y_i^{(k+1)}, \quad (i=1,\ldots,6,\; k=1,2,3), \end{array}$$ and the boundary conditions $$ \begin{array}{lll} y_1^{(1)}(0) = 1.5776, & y_2^{(1)}(0) = 8.32, & y_3^{(1)}(0) = 0, \\ y_4^{(1)}(0) = 0, & y_5^{(1)}(0) = 0, & y_6^{(1)}(0)-p = 0, \\ & y_4^{(3)}(t_f^{(3)}) \leq 1.
\end{array}$$ The solution of the kinetic batch reactor problem using GPOPS-II with the NLP solver IPOPT is shown in the figures below.

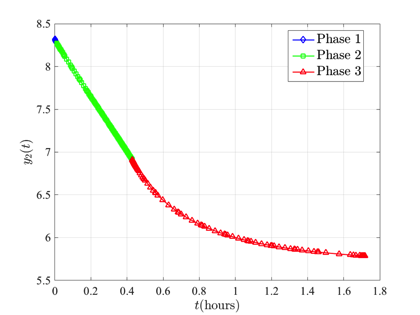

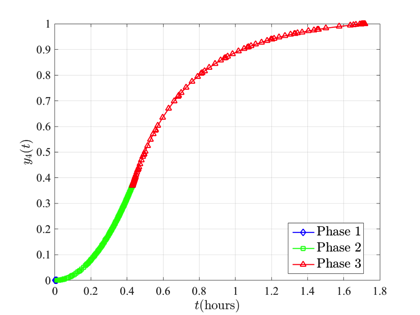

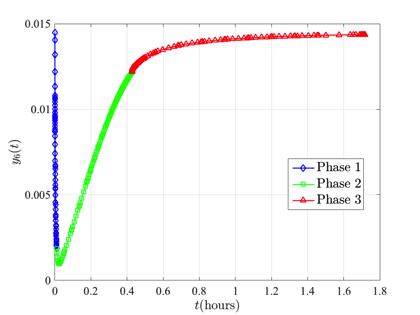


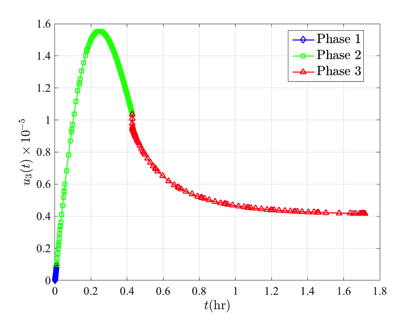


Image Courtesy of Process Engineering Associates, LLC. Used by Permission. Original Image Found at http://www.processengr.com/case_summaries/case_images/sii/batch_reactor.jpg.

